Equivalent variation
Equivalent variation (EV) is a measure of how much more money a consumer would pay before a price increase to avert the price increase. Because the meaning of "equivalent" may be unclear, it is also called extortionary variation. John Hicks (1939) is attributed with introducing the concept of compensating and equivalent variation.
It is a useful tool when the present prices are the best place to make a comparison.
The value of the equivalent variation is given in terms of the expenditure function (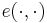 ) as
) as
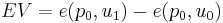
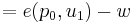
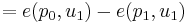
where  is the wealth level,
is the wealth level, 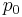 and
and 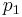 are the old and new prices respectively, and
are the old and new prices respectively, and 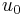 and
and 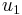 are the old and new utility levels respectively.
are the old and new utility levels respectively.
Value function form
Equivalently, in terms of the value function (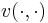 ),
),
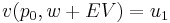
This can be shown to be equivalent to the above by taking the expenditure function of both sides at 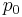
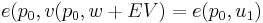

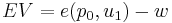
One of the three identical equations above.
See also
Compensating variation (CV) is a closely related measure of welfare change.
References
- Mas-Colell, A., Whinston, M and Green, J. (1995) Microeconomic Theory, Oxford University Press, New York.